将行转换为列或将列转换为行称为矩阵的C转置。如何在此编程语言中使用示例编写程序来转置矩阵。
C语言矩阵转置示例
此矩阵转置程序允许用户输入二维数组的行数和列数。然后,C程序将把行转换为列,反之亦然,这也称为矩阵转置。
#include<stdio.h>
int main()
{
int i, j, rows, columns, a[10][10], b[10][10];
printf("\nPlease Enter Number of rows and columns\n");
scanf("%d %d", &i, &j);
printf("\n Please Enter the Array Elements \n");
for(rows = 0; rows < i; rows++)
{
for(columns = 0;columns < j; columns++)
{
scanf("%d", &a[rows][columns]);
}
}
for(rows = 0; rows < i; rows++)
{
for(columns = 0;columns < j; columns++)
{
b[columns][rows] = a[rows][columns];
}
}
printf("\n Transpose Matrix Elemnts are: \n");
for(rows = 0; rows < j; rows++)
{
for(columns = 0; columns < i; columns++)
{
printf("%d \t ", b[rows][columns]);
}
printf("\n");
}
return 0;
}
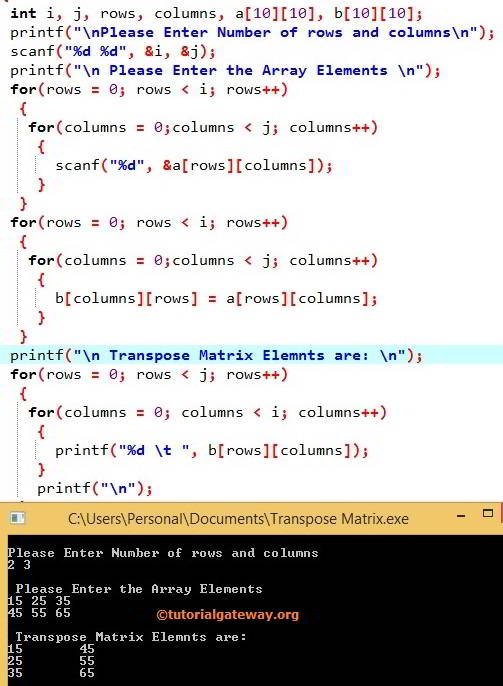
在此C语言矩阵转置程序中,我们声明了两个大小为10*10的二维数组a和b。第一个printf语句要求用户输入二维数组a、b的大小(行数和列数。例如,2行3列=a[2][3])。
C语言的scanf语句会将用户输入的值赋给i和j(行=i,列=j)。
此程序中的第一个for循环将帮助迭代a[2][3]矩阵中的每个单元格。for循环内的条件((rows < i) and (columns < j))将确保编译器不会超出限制。否则,它将溢出。
for循环内的scanf语句将用户输入的值存储在每个单独的数组元素中,例如a[0][0],a[0][1],a[0][2],a[1][0],a[1][1],a[1][2]。
在下一行,我们有另一个for循环。而上面的for循环用于转置矩阵a[2][3]并将其放入b。
从上面的截图来看,用户为矩阵转置示例插入的值为:
a[2][3] = { {15, 25, 35}, { 45, 55, 65} }
行第一次迭代
行值为0,条件(0 < 2)为True。因此,它将进入第二个for循环。
矩阵列转置第一次迭代
列值为0,条件(0 < 2)为True。
b[columns][rows] = a[rows][columns] => a[0][0]
b[0][0] = 15
列第二次迭代
columns = 1,条件(1 < 3)为True。由于我们没有退出内部循环(列循环),因此行值将为0。
b[1][0] = a[0][1]
b[1][0] = 25
列第三次迭代
col = 2,条件(2 < 3)为True。
b[2][0] = a[0][2]
b[2][0] = 35
增加后,列值将为3,条件(3 < 3)将失败。因此,它将退出循环。
现在行值将增加,开始C语言矩阵转置的第二次迭代。
行第二次迭代
行值为1,条件(1 < 2)为True。因此,它将进入第二个for循环。
列第一次迭代
列值为0,条件(0 < 3)为True。
b[0][1] = a[1][0]
b[0][1] = 45
列第二次迭代
column = 1,条件(1 < 3)为True。我们仍在内部循环中,因此行值为1。
b[1][1] = a[1][1]
b[1][1] = 55
矩阵转置列第三次迭代
cols = 2,条件(2 < 3)为True。
b[2][1] = a[1][2]
b[2][1] = 65
增加后,cols的值将为3,条件(columns < 3)将失败。因此,它将退出循环。
现在行值将增加,这意味着2,条件(2 < 2)将失败。因此,它将退出循环。
在C语言中转置矩阵后,a[2][3]将变为b[3][2]。
接下来的for循环将按上述方式进行遍历。尽管进行了转置,但它使用printf语句逐个显示值。
如果观察此示例中的for循环,我们将行分配给j,将列分配给i。因为最初,用户输入的值是2行3列。转置矩阵后,它变成了3行2列。这就是为什么我们将j值赋给行,将i值赋给列。如果不是动态程序,请将常量值直接放在i和j的位置。
最终输出为:b[3][2] = { {15, 45}, {25, 55}, {35, 65} };