R 编程中的递归函数

R 编程语言引入了一种称为递归或递归函数的新技术，用于优雅而简洁的编码。递归是指函数调用自身。在本文中，我们将通过实际示例展示如何使用递归函数编写简单的程序。

为了理解 R 递归函数编程，让我们考虑一个众所周知且简单的示例——阶乘。我们可以使用以下公式计算任何给定数字的阶乘。

n! = (n) * (n-1) * (n-2) * ….. * 1

这意味着，6! = 6 * 5 * 4 * 3 * 2 * 1

我们可以在 R 编程中使用 For 循环、While 循环等来实现。但如果您观察到上述模式，其行为是重复的，这意味着它是递归的。因此，我们不必编写循环（成本高昂），而是可以编写 R 编程的递归函数。

# Example
Number.factorial <- function(number)
{
  if(number == 0 || number == 1) {
    return (1)
  } else {
    return (number *  Number.factorial(number - 1))
  }
}
Sum.Series(6)
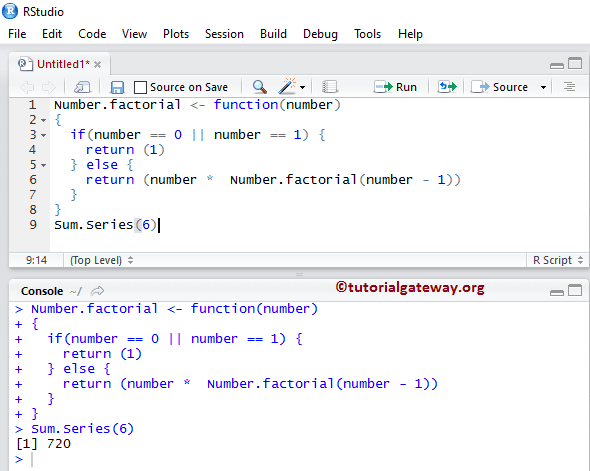
Recursive Functions in R Programming 1

如果我们将 0 或 1 作为 Number 参数值传递，那么 R 递归函数将返回 1，否则，它将返回以下语句。

(number *  Number.factorial(number - 1))

让我们计算 6！

6! = number *  Number.factorial(number - 1)

   = 6 * Number.factorial (6 -1) 

   = 6 * Number.factorial (5) # Recursively calling the above function

   = 6 * 5 * Number.factorial (5 -1)

   = 6 * 5 * Number.factorial (4) # Recursively calling the above function

   = 6 * 5 * 4 * Number.factorial (4 -1)

   = 6 * 5 * 4 * Number.factorial (3) # Recursively calling the above function

   = 6 * 5 * 4 * 3 * Number.factorial (3 -1)

   = 6 * 5 * 4 * 3 * Number.factorial (2) # Recursively calling the above function

   = 6 * 5 * 4 * 3 * 2 * Number.factorial (2 -1)

   = 6 * 5 * 4 * 3 * 2 * Number.factorial (1) # Recursively calling the above function

   = 6 * 5 * 4 * 3 * 2 * 1

   = 720

在 R 中使用递归函数查找级数 1²+2²+3²+…..+n² 的和

在此示例中，我们将展示如何使用此编程中的递归函数编写程序来查找级数 1²+2²+3²+…..+n² 的和。请参考For 循环和While 循环文章。

# Example
Sum.Series <- function(number)
{
  if(number == 0) {
    return (0)
  } else {
    return ((number * number ) + Sum.Series(number - 1))
  }
}
Sum.Series(5)
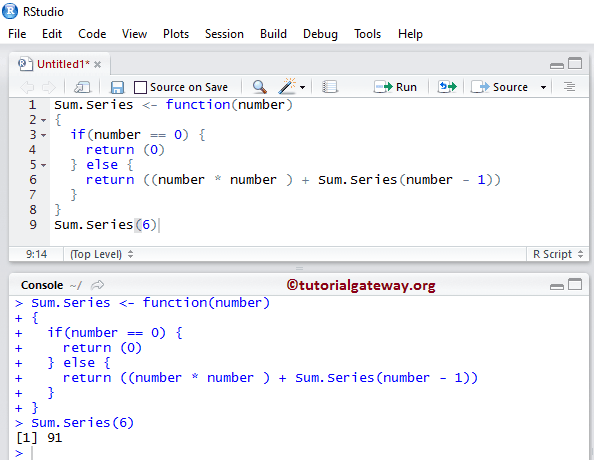
Recursive Functions 2

让我向您展示递归函数的逐步执行过程。

函数定义：在 Sum.Series (number) 函数内，

如果用户输入的 Number 是 0，则函数返回 0，否则，它返回以下内容

(number * number ) + Sum.Series(number - 1)

为了更好地理解，让我们分解上面的表达式

  • (number * number) = 将数字相乘
  • Sum.Series(number – 1) = 使用递减值（数字减 1）调用同一个函数

从上面 R 递归函数示例的屏幕截图中，您可以看到用户输入的值是 6

递归 1：number = 6，大于 0

  • (number * number ) + Sum.Series(number – 1)
  • (6 * 6) + Sum.Series(6 – 1)
  • 36 + Sum.Series(5)

2：number 变为 5，大于 0

  • (number*number ) + Sum.Series(number – 1)
  • (5 * 5) + Sum.Series(5 – 1)
  • 25 + Sum.Series(4)

总和将是 36 + 25 = 61

迭代 3：number 变为 4，大于 0

  • (4 * 4) + Sum.Series(4 – 1)
  • 16 + Sum.Series(3)

总和为 36 + 25 + 16 = 77

递归 4：number 变为 3，大于 0，所以，

  • (3 * 3) + Sum.Series(3 – 1)
  • 9 + Sum.Series(2)

总和 = 36 + 25 + 16 + 9 = 86

递归 5：number 变为 2，大于 0，所以

  • (2 * 2) + Sum.Series(2 – 1)
  • 4 + Sum.Series(1)

总和将是 36 + 25 + 16 + 9 + 4 = 90

递归 6：number 变为 1，大于 0。

  • (1 * 1) + Sum.Series(1 – 1)
  • 1 + Sum.Series(0)

总和 = 36 + 25 + 16 + 9 + 4 + 1 = 91

递归 7：number 变为 0，这意味着第一个 if 条件为 True，函数退出。

最终输出是 91

我们必须使用一些条件来退出递归函数调用。如果您忘记了条件，那么函数将执行无数次（类似于无限循环）。