R中的矩阵是最二维的数据结构。在矩阵中,数据以行和列的形式存储,我们可以使用行索引和列索引来访问元素(类似于Excel文件)。让我们看看如何创建矩阵、如何访问和操作元素以及如何进行算术运算,并附带示例。
R编程中矩阵的语法如下所示。
Matrix_Name <- matrix(data, nrow, ncol, byname, dimnames)
如果您观察到上述语法,数据是一个向量,并且
- nrow 是您要创建的行数。例如,nrow = 3 将创建一个3行R矩阵。
- ncol:您要创建的列数。例如,ncol = 2 将创建一个2列的矩阵。
- byrow:默认情况下为FALSE。如果为TRUE,则元素将按行排列。
- dimnames:用于将默认的行名和列名更改为更有意义的名称。
在R中创建矩阵
在此示例中,我们将创建一个包含12个元素的矩阵。创建矩阵最传统的方法是
A <- matrix(c(1:12), nrow = 3, ncol = 4) print(A) # Elements are arranged sequentially by column. B <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = FALSE) print(B) # Elements are arranged sequentially by row. D <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = TRUE) print(D)
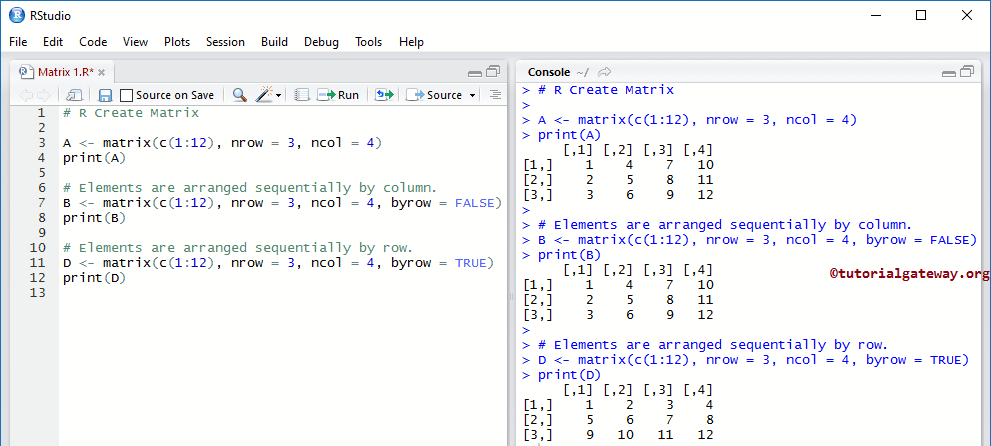
它创建了一个包含12个元素的矩阵,这些元素排列成三行四列。
A <- matrix(c(1:12), nrow = 3, ncol = 4)
正如您所见,元素是按列排列的。为了显示这一点,我们明确指定了 byrow 参数。
B <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = FALSE)
让我们将byrow选项从FALSE更改为TRUE,以按行排列元素。
D <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = TRUE)
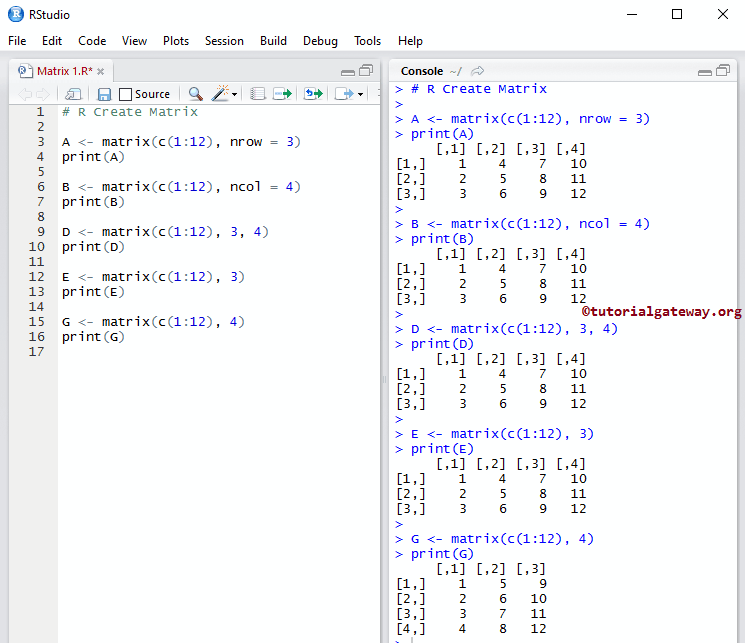
在R中创建矩阵的简单方法
在R编程中,并非总是需要指定nrow和ncol。
# It will create a Matrix of 3 Rows and the remaining items will be arranged Accordingly A <- matrix(c(1:12), nrow = 3) print(A) # It will create 4 Columns and the remaining (row) items will be arranged Accordingly B <- matrix(c(1:12), ncol = 4) print(B) # It will create 3 rows and 4 Columns D <- matrix(c(1:12), 3, 4) print(D) # It will create a 3 rows E <- matrix(c(1:12), 3) print(E) # It will create 4 Rows. To create 4 Columns you have to specify ncol = 4 explicitly G <- matrix(c(1:12), 4) print(G)
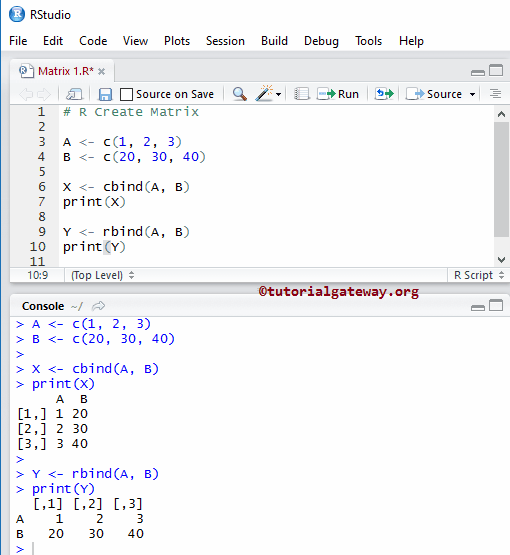
使用cbind和rbind创建矩阵
本示例展示了另一种在编程中创建矩阵的方法。cbind用于按列绑定向量,而rbind用于按行绑定向量。
A <- c(1, 2, 3) B <- c(20, 30, 40) X <- cbind(A, B) print(X) Y <- rbind(A, B) print(Y)
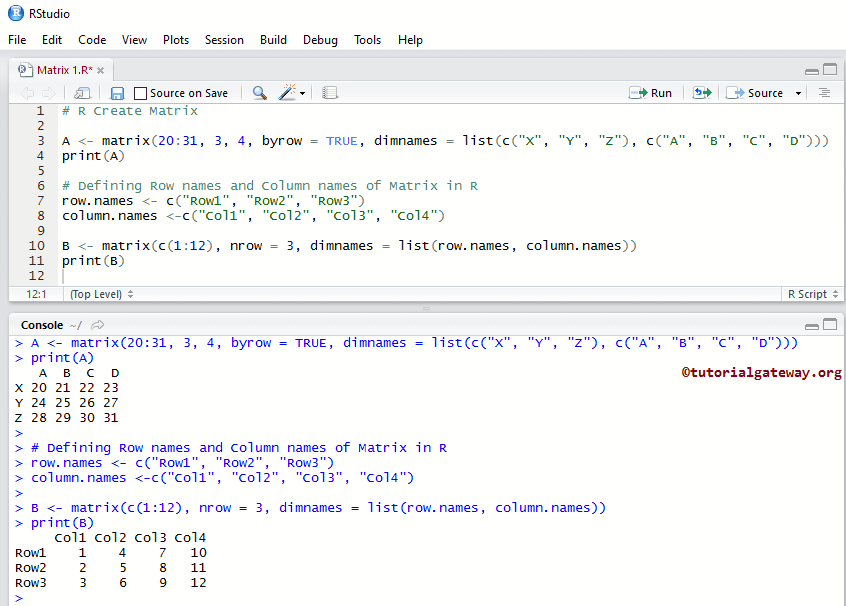
为R中的矩阵定义行名和列名
我们将替换行和列的默认名称,或为行和列定义新名称。我们可以使用dimnames以这种方式实现:x <- matrix(1:12, 4, 3, dimnames = list(rowNames, columnNames)
A <- matrix(20:31, 3, 4, byrow = TRUE, dimnames = list(c("X", "Y", "Z"), c("A", "B", "C", "D")))
print(A)
# Defining names
row.names <- c("Row1", "Row2", "Row3")
column.names <-c("Col1", "Col2", "Col3", "Col4")
B <- matrix(c(1:12), nrow = 3, dimnames = list(row.names, column.names))
print(B)
具有循环元素的矩阵
上面的示例工作正常,因为我们指定了确切的行和列元素,例如12个元素排列成3行4列。如果我们指定较少数量的元素会怎样?
A <- matrix(c(44: 46), nrow = 3, ncol = 3) print(A) B <- matrix(c(44: 46), nrow = 3, ncol = 3, byrow = TRUE) print(B)
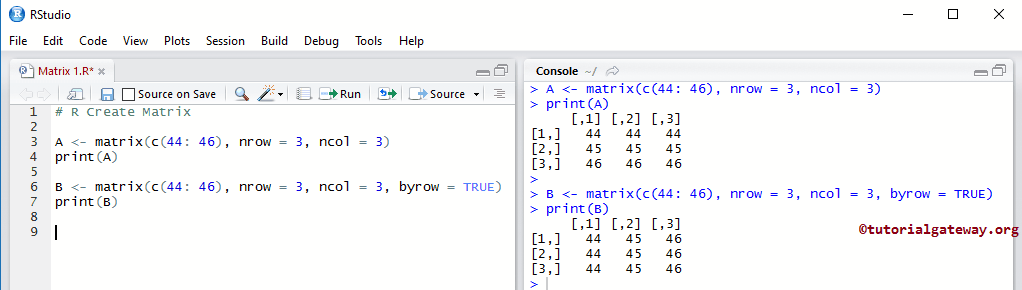
它创建了一个包含12个项目的矩阵,这些项目排列成三行四列。这里,44、45和46将重复使用,直到创建完3*4的矩阵为止。
A <- matrix(c(44: 46), nrow = 3, ncol = 3)
这里,44、45和46是按列排列的。为了改变循环样式,我们已将byrow选项从FALSE更改为TRUE。这将按行排列元素。
B <- matrix(c(44: 46), nrow = 3, ncol = 3, byrow = TRUE)
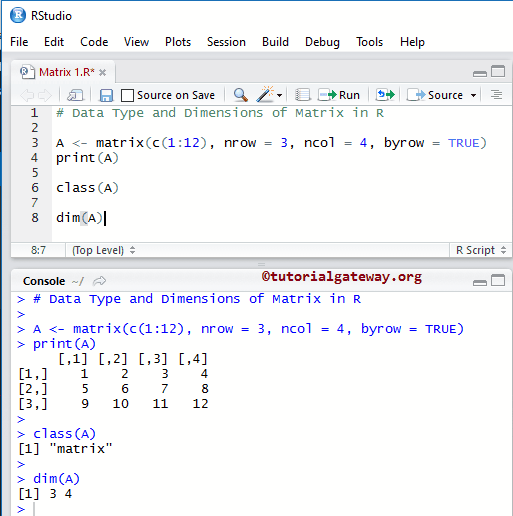
矩阵的重要函数
在此编程中,Class函数将定义其类型,而dim函数将返回矩阵的维度。
# Data Type and Dimensions A <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = TRUE) print(A) class(A) dim(A)
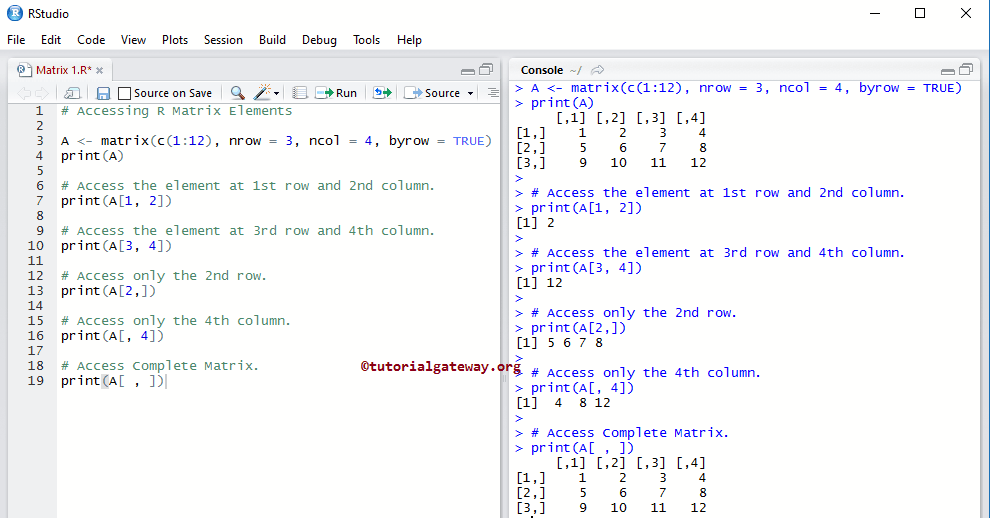
访问R矩阵元素
在此编程中,我们可以使用索引位置来访问矩阵元素。使用此索引值,我们可以更改每个元素。索引从1开始,到n结束,其中n是行或列的大小。
例如,我们声明一个6*4的矩阵,这意味着它将存储6个行元素和4个列元素。要访问或修改第1个值,请使用Matrix.name[1, 1];要访问或修改第2行第3列的值,请使用Matrix.name[2, 3];要访问第6行第4列,请使用Matrix.name[6, 4]。
# Accessing Items A <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = TRUE) print(A) # Access the Items at 1st row and 2nd column. print(A[1, 2]) # Access the items at 3rdrow and 4thcolumn. print(A[3, 4]) # Access only the 2ndrow. print(A[2,]) # Access only the 4th column. print(A[, 4]) # Access All print(A[ , ])
访问矩阵的子集
在这里,我们展示了如何从中访问多个项目的子集。为此,我们使用向量。负索引位置用于省略这些值。
# Accessing Items Subset A <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = TRUE) print(A) # Access the Items at 1st, 3rd row and 2nd, 4th column. print(A[c(1, 2), c(3, 4)]) # Access All the element at 2nd and 3rd row. print(A[c(2, 3), ]) # Access All the element at 1st and 4th Column. print(A[ , c(1, 4)]) # Access All the element except 2nd row. print(A[-2, ]) # Access All the items except 2ndrow and 3rdColumn. print(A[-2, -3]) # Access All the element except 3rd and 4th Column. print(A[, c(-3, -4)])
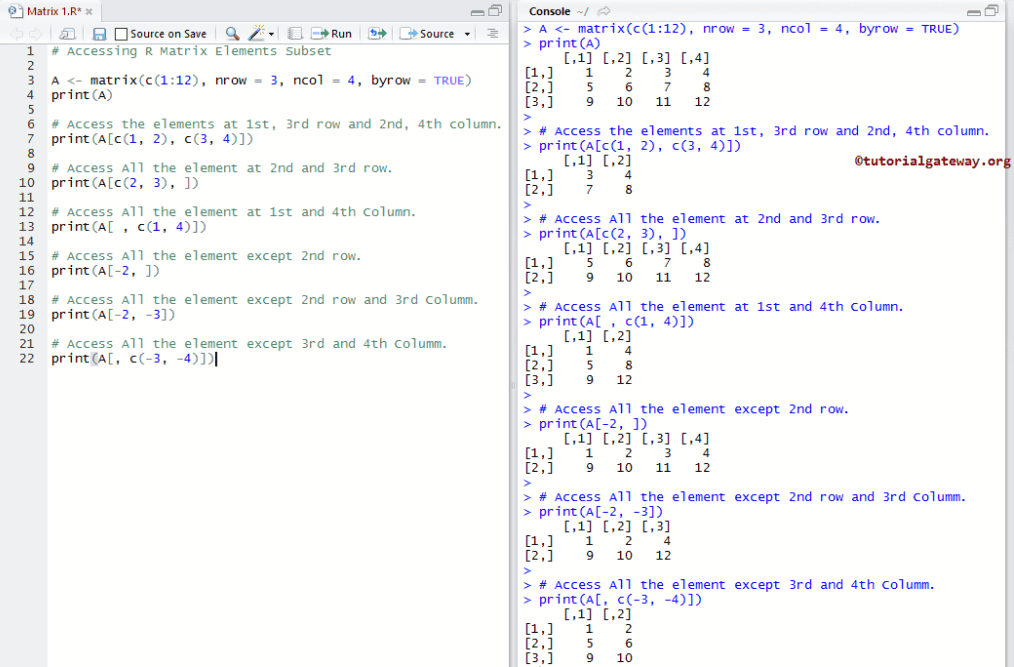
使用布尔向量访问矩阵元素
在此示例中,我们声明了一个布尔向量。我们使用这些布尔值作为索引位置来访问R矩阵元素。这里,TRUE表示访问该值,FALSE表示省略。
# Accessing Elements using Boolean Vector A <- matrix(c(1:12), nrow = 3, ncol = 4, byrow = TRUE) print(A) # Access the elements at 1st, 3rd row and 2nd, 4th column. print(A[c(TRUE, FALSE, TRUE), c(FALSE, TRUE, FALSE, TRUE)]) # Access All the element at 1ST AND 2nd row. print(A[c(TRUE, TRUE, FALSE), ]) # Access All the element at 1st and 4th Column. print(A[ , c(FALSE, TRUE)]) # Access the elements at 1st, 2nd row and 2nd, 4th column. print(A[c(1, 2), c(FALSE, TRUE, FALSE, TRUE)])
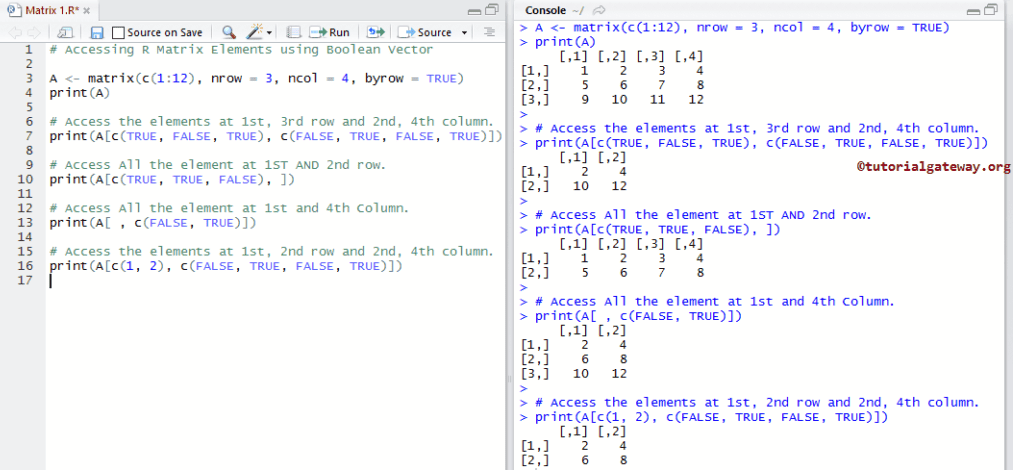
使用字符索引访问R矩阵元素
它显示了如何使用字符向量索引值来访问矩阵元素。在这里,我们分配了行名和列名,这可以帮助我们使用行名作为索引值来提取项目。
# Accessing Elements using Char Index
# Defining Row names and Column names of Matrix in R
row.names <- c("Row1", "Row2", "Row3")
column.names <-c("Col1", "Col2", "Col3", "Col4")
B <- matrix(c(1:12), nrow = 3, dimnames = list(row.names, column.names))
print(B)
# Access the elements at 1st row and 3rd Column.
print(B["Row1", "Col3"])
# Access only the 2nd row.
print(B["Row2",])
# Access only the 4th column.
print(B[, "Col4"])
# Access the elements at 2nd row and 2, 3, 4th Column.
print(B["Row2", 2:4])
# Access the elements at 1st, 3rd row and 1, 2, 3rd Column.
print(B[c("Row1", "Row2"), 2:4])
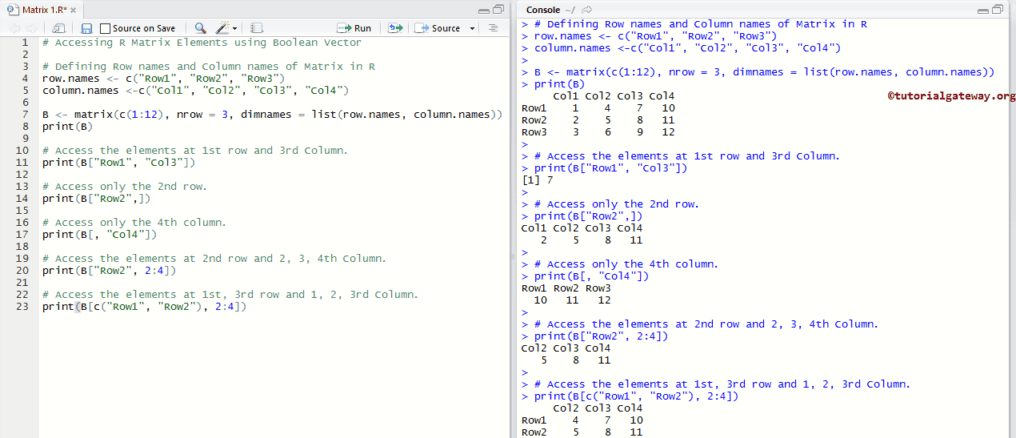
修改矩阵元素
在编程中,我们可以使用索引位置来修改矩阵中的元素。例如,如果我们声明一个3*4的矩阵,可以存储12个元素(3行4列)。要访问或修改第1个值,请使用MatrixName[1, 1]。要访问或修改第2行第3列的值,请使用MatrixName[2, 3]。
# Modifying A <- matrix(c(1:9), nrow = 3, ncol = 3) print(A) A[2, 2] <- 100 print(A) A[A < 5] <- 222 print(A)
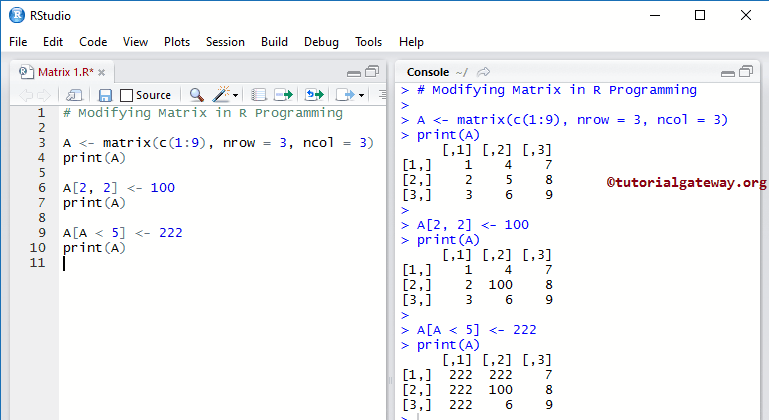
它将100赋给第2行第2列位置的元素。
A[2, 2] <- 100
它将222赋给所有值小于5的元素。这里A < 5将检查A中的元素是否小于5,如果条件为真,则该元素将被222替换。
A[A < 5] <- 222
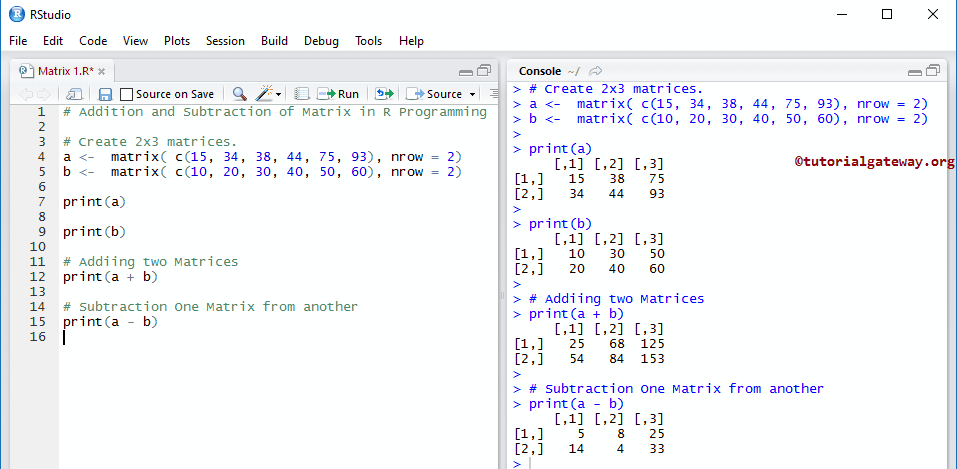
矩阵加法和减法
使用算术运算符在R编程中对矩阵执行算术运算。
# Addition and Subtraction # Create 2x3 matrices. a <- matrix( c(15, 34, 38, 44, 75, 93), nrow = 2) b <- matrix( c(10, 20, 30, 40, 50, 60), nrow = 2) print(a) print(b) # Adding two print(a + b) # Subtraction One from another print(a - b)
这里,a + b 表示 (15 + 10, 34 + 20, 38 + 30, 44 + 40, 75 + 50, 93 + 60)
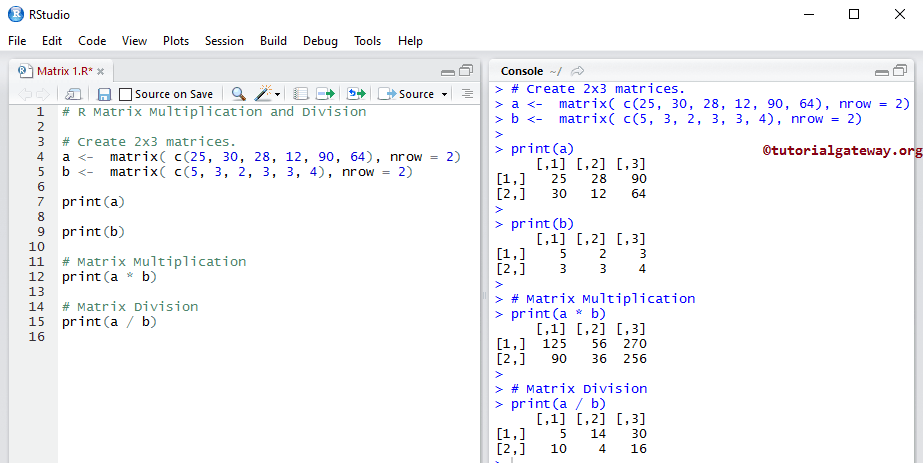
矩阵乘法和除法
我们使用算术运算符来执行矩阵乘法和除法。首先,我们声明了a和b,它们是两行三列。
接下来,我们对它们执行了矩阵乘法和除法。这里a * b表示(25 * 5, 30 * 3, 28 * 2, 12 * 3, 90 * 3, 64 * 4),而a / b表示(25 / 5, 30 / 3, 28 / 2, 12 / 3, 90 / 3, 64 / 4)。
# Multiplication and Division # Create 2x3 matrices. a <- matrix( c(25, 30, 28, 12, 90, 64), nrow = 2) b <- matrix( c(5, 3, 2, 3, 3, 4), nrow = 2) print(a) print(b) # Multiplication print(a * b) # Division print(a / b)