Python 程序查找两个数的 GCD

编写一个 Python 程序，使用 While 循环、函数和递归来查找两个数的 GCD。要查找 GCD 或 HCF，我们必须至少传递一个非零值。

最大公约数也称为最高公因子（HCF）、最大公因子（GCF）、最高公约数（HCD）或最大公约数（GCM）。

在数学中，两个或多个整数的最大公约数是能整除给定整数值而没有余数的最大正整数。例如，整数 8 和 12 的 GCD 值是 4，因为 8 和 12 可以被 1、2 和 4 整除（余数为 0），其中最大的正整数是 4。

使用 while 循环查找两个数 GCD 的 Python 程序

此 Python 程序允许用户输入两个正整数值。接下来，我们使用 While 循环来限制 i 值不大于用户指定的值。

在 While 循环中，我们使用 If 语句检查 a%i 和 a % i 的余数是否等于零。如果为真，则最高公因子 = i；否则，跳过该值。

a = float(input(" Please Enter the First Value a: "))
b = float(input(" Please Enter the Second Value b: "))

i = 1
while(i <= a and i <= b):
    if(a % i == 0 and b % i == 0):
        val = i
    i = i + 1
    
print("\n HCF of {0} and {1} = {2}".format(a, b, val))

这是查找 HCF 或 GCD 的另一种方法，使用 while 循环查找两个数的最大公因子。在此 程序 中，我们使用 Temp 变量来查找 GCD。

num1 = float(input(" First : "))
num2 = float(input(" Second : "))

a = num1
b = num2

while(num2 != 0):
    temp = num2
    num2 = num1 % num2
    num1 = temp

hcf = num1   
print("\n HCF of {0} and {1} = {2}".format(a, b, hcf))

 First : 12
 Second : 36

 HCF of 12.0 and 36.0 = 12.0

使用 gcd 函数查找两个数 HCF 的程序

有一个内置的数学函数叫做 gcd() 函数，它接受两个参数并返回它们的 HCF。此函数只接受整数值。

import math

a = int(input("First : "))
b = int(input("Second : "))

hcf = math.gcd(a, b)

print(hcf)

First : 30
Second : 18
6

不使用 Temp 查找两个数 GCD 的 Python 程序

在此程序中，我们不使用 Temp 变量来查找两个数的 GCD。它使用算术减法运算符将一个变量减去另一个变量并找到结果。

num1 = float(input(" First : "))
num2 = float(input(" Second : "))

a = num1
b = num2

if(num1 == 0):
    print("\n HCF of {0} and {1} = {2}".format(a, b, b))

while(num2 != 0):
    if(num1 > num2):
        num1 = num1 - num2
    else:
        num2 = num2 - num1

hcf = num1   
print(hcf)

 First : 75
 Second : 255

 HCF of 75.0 and 255.0 = 15.0

使用 for 循环查找两个数 GCD 的程序

此程序使用 for 循环迭代从 1 到两者之间较小的数。接下来，我们找到 num1 和 num2 变量的除数，并将最大值存储在 result 变量中。

num1 = int(input("First  : "))
num2 = int(input("Second : "))

for i in range(1, min(num1, num2) + 1):
    if num1 % i == 0 and num2 % i == 0:
        result = i

print(result)

使用函数查找两个数 GCD 的 Python 程序

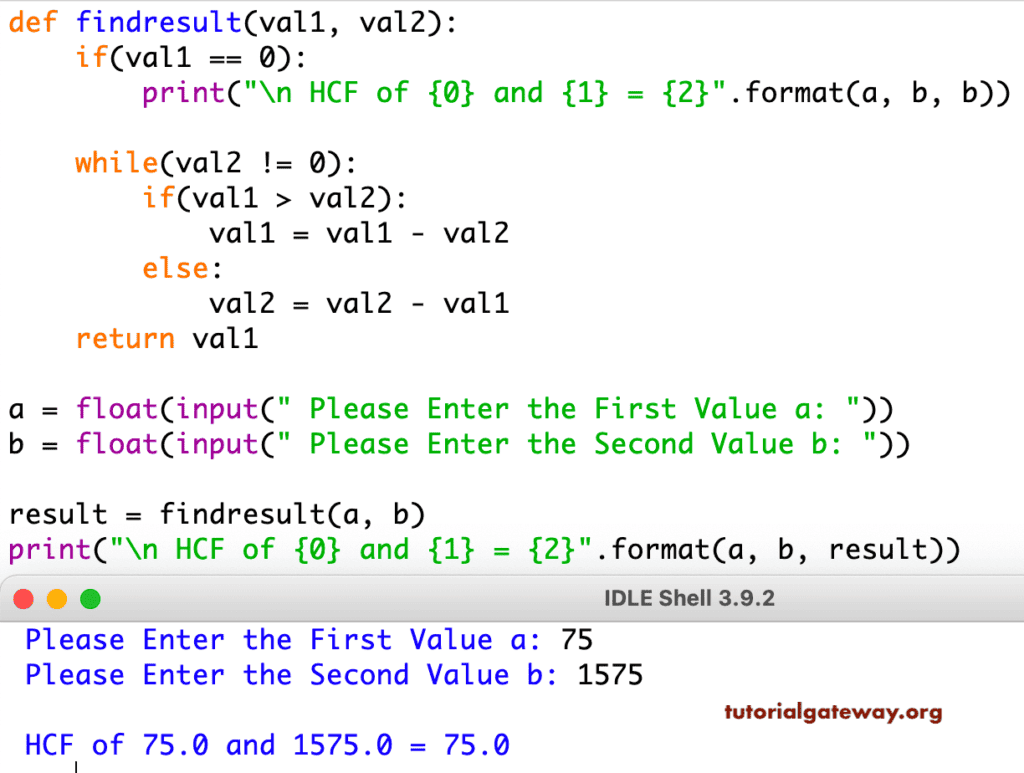
此 Python 程序与上面相同。但是，我们使用 函数 来分离逻辑。

def findresult(val1, val2):
    if(val1 == 0):
        print("\n HCF of {0} and {1} = {2}".format(a, b, b))

    while(val2 != 0):
        if(val1 > val2):
            val1 = val1 - val2
        else:
            val2 = val2 - val1
    return val1

a = float(input(" Please Enter the First Value a: "))
b = float(input(" Please Enter the Second Value b: "))

result = findresult(a, b)  
print("\n HCF of {0} and {1} = {2}".format(a, b, result))

我们可以尝试以下代码来查找最大公约数或最高公因子。您可以使用赋值运算符 (=) 为多个变量赋值，而不是编写 If else 条件。

def calgcd(a, b):
    while (b):
        a, b = b, a % b
    return a

x = float(input("First : "))
y = float(input("Second : "))

hcf = calgcd(x, y)

print("Result =", hcf)

First : 98
Second : 77
Result = 7.0

使用递归查找两个数 GCD 的 Python 程序

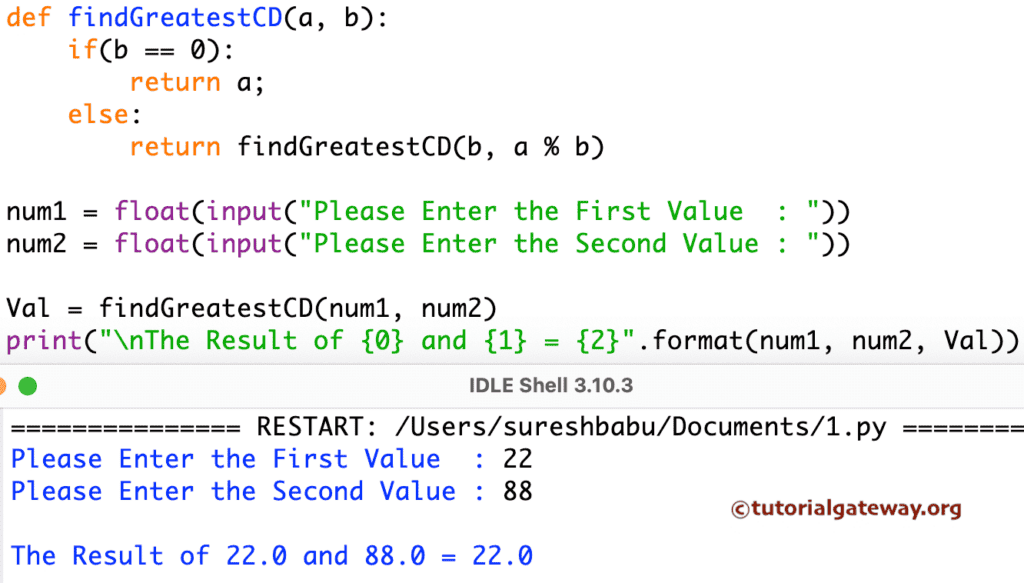
它允许用户输入两个正整数值，并通过递归调用 findGreatestCD 函数来计算这两个值的最大公约数。

def findGreatestCD(a, b):
    if(b == 0):
        return a;
    else:
        return findGreatestCD(b, a % b)
    
num1 = float(input(" Please Enter the First Value  : "))
num2 = float(input(" Please Enter the Second Value : "))

Val = findGreatestCD(num1, num2)
print("\n The Result of {0} and {1} = {2}".format(num1, num2, Val))

如何使用三元运算符查找 HCD 或 HCF？

此示例帮助您在一行中编写完整的代码。

def findHCF(a, b):
    return a if b == 0 else findHCF(b, a % b)

num1 = float(input("Enter the First Value  : "))
num2 = float(input("Enter the Second Value : "))

print(findHCF(num1, num2))

Enter the First Value  : 76
Enter the Second Value : 128
4.0

使用约简算法的两个数的 GCD

此示例借助 if 语句使用了约简算法方法。

def findHCF(a, b):
    if a == 0:
        return b
    if b == 0:
        return a
    if a == b:
        return a
    if a > b:
        return findHCF(a - b, b)
    return findHCF(a, b - a)

num1 = float(input("Enter the First Value  : "))
num2 = float(input("Enter the Second Value : "))

print(findHCF(num1, num2))

Enter the First Value  : 22
Enter the Second Value : 44
22.0