Java 程序查找矩阵对角线之和

编写一个 Java 程序，通过示例查找矩阵对角线项之和，或计算对角线项的多维数组之和。

在此矩阵对角线项之和示例中，我们声明了一个具有随机值的 3*3 整型 Sod_arr。接下来，我们使用 for 循环迭代 Sod_arrMatrix 项。在 for 循环 中，我们正在计算 Sod_arr 中对角线项的和。

public class SumOfDiagonals {
	
	public static void main(String[] args) {
		
		int i, sum = 0;	
	
		int[][] Sod_arr = {{15, 25, 35}, {45, 55, 65}, {75, 85, 95}};
	
		for(i = 0; i < Sod_arr.length ; i++)
		{
				sum = sum + Sod_arr[i][i];
		}
	System.out.println("\nThe Sum of the Diagonal Items = " + sum);

	}
}

The Sum of the Diagonal Items = 165

Java 程序查找矩阵对角线项之和示例 2

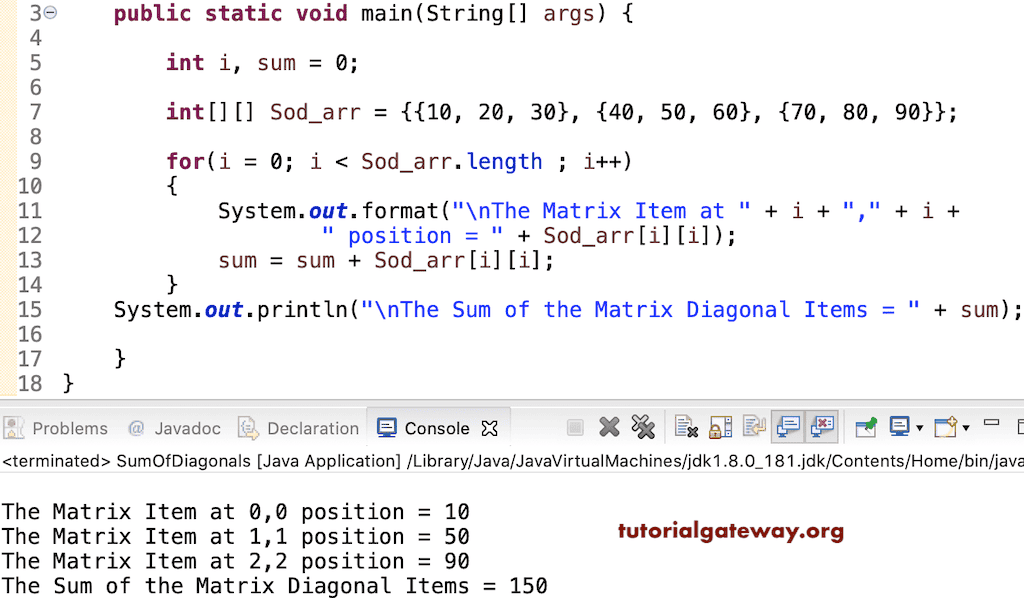
此矩阵对角线项之和代码与上述代码相同。但是，在此我们添加了一个额外的语句来显示对角线位置的值。

public class SumOfDiagonals {
	
	public static void main(String[] args) {
		
		int i, sum = 0;	
	
		int[][] Sod_arr = {{10, 20, 30}, {40, 50, 60}, {70, 80, 90}};
	
		for(i = 0; i < Sod_arr.length ; i++)
		{
			System.out.format("\nThe Matrix Item at " + i + "," + i +
					" position = " + Sod_arr[i][i]);
			sum = sum + Sod_arr[i][i];
		}
	System.out.println("\nThe Sum of the Matrix Diagonal Items = " + sum);

	}
}

此 Java 代码 与上面的 Java 代码相同。但是，此矩阵对角线之和代码允许用户输入行数、列数和项。

import java.util.Scanner;

public class SumOfDiagonals {
	private static Scanner sc;
	
	public static void main(String[] args) {
		
		int i, j, rows, columns, sum = 0;
		
		sc= new Scanner(System.in);
		
		System.out.println("\n Enter Rows and Columns :  ");
		rows = sc.nextInt();
		columns = sc.nextInt();
		
		int[][] Sod_arr = new int[rows][columns];
		
		System.out.println("\n Please Enter the Items :  ");
		for(i = 0; i < rows; i++) {
			for(j = 0; j < columns; j++) {
				Sod_arr[i][j] = sc.nextInt();
			}		
		}
	
		for(i = 0; i < Sod_arr.length ; i++)
		{
			System.out.format("\nThe Item at " + i + "," + i +
					" position = " + Sod_arr[i][i]);
			sum = sum + Sod_arr[i][i];
		}
	System.out.println("\nThe Sum of the Matrix Diagonal Items = " + sum);

	}
}

 Enter Rows and Columns :  
3 3

 Please Enter the Items :  
11 22 33
44 55 66
77 88 99

The Item at 0,0 position = 11
The Item at 1,1 position = 55
The Item at 2,2 position = 99
The Sum of the Matrix Diagonal Items = 165