Java 程序查找两个数的 GCD

编写一个 Java 程序，使用 For 循环、While 循环和递归方法查找两个数的 GCD。最大公约数也称为最高公因子 (HCF)、最高公约数 (HCD)、最大公因子 (GCF) 或最大公约数 (GCM)。

根据数学，两个或多个整数的 GCD 是能将给定整数整除且没有余数的最大正整数。例如，8 和 12 的 GCD 是 4，因为 8 和 12 可以被 1、2 和 4 整除。在因子 1、2 和 4 中，最大的正整数是 4。

使用 For 循环查找两个数 GCD 的 Java 程序

此 Java 程序允许用户输入两个正整数值。然后，它使用 For 循环 计算这两个值的最高公因子 (HCF)。

注意：要查找最大公约数，我们必须至少提供一个非零值。

import java.util.Scanner;

public class GCDofTwo1 {
	private static Scanner sc;
	public static void main(String[] args) 
	{
		int Num1, Num2, i, GCD = 0;
		sc = new Scanner(System.in);
		
		System.out.print(" Please Enter the First Integer Value : ");
		Num1 = sc.nextInt();	
		
		System.out.print(" Please Enter the Second Integer Value : ");
		Num2 = sc.nextInt();
		
		for(i = 1; i <= Num1 && i <= Num2; i++)
	    {
	        if(Num1 % i == 0 && Num2 % i == 0)
	        {
	            GCD = i;
	        }
	    }	
		System.out.println("\n GCD of " + Num1 + " and " + Num2 + "  =  " + GCD);
	}
}

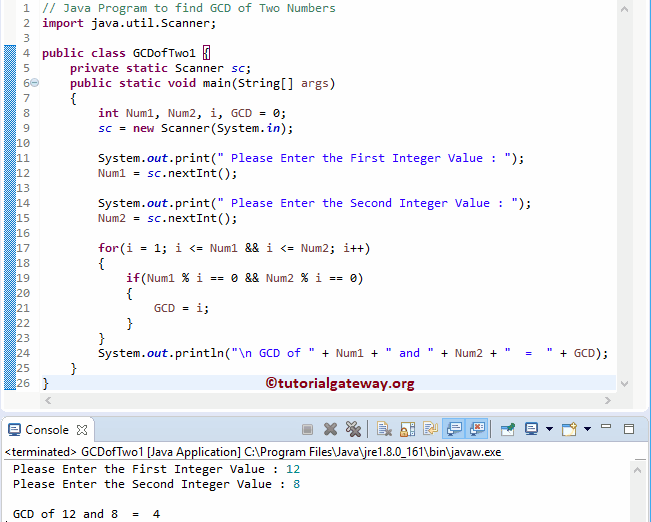
查找两个数 GCD 的程序分析如下。

Num1 = 12, Num2 = 8，for 循环条件为 for( i = 1; i <= 12 && i <= 8; i++)。

第一次迭代：i = 1

if(12 % 1 == 0 && 8 % 1 == 0) 为 True。所以 GCD = 1

第二次迭代：i = 2

if(12 % 2 == 0 && 8 % 2 == 0) 为 True。所以 GCD = 2

第三次迭代：i = 3

if(12 % 3 == 0 && 8 % 3 == 0) 为 False。

第四次迭代：i = 4

if(12 % 4 == 0 && 8 % 4 == 0) 为 True。所以它是 4

对于所有剩余的迭代，条件都变为 False。所以，最终输出是 4。

使用 While 循环查找两个数 GCD 的 Java 程序

在此程序中，我们使用 While 循环和临时变量 (temp) 来计算两个数的 GCD。

import java.util.Scanner;

public class GOT2 {
	private static Scanner sc;
	public static void main(String[] args) 
	{
		int Num1, Num2, Temp, GCD = 0;
		sc = new Scanner(System.in);
		
		System.out.print(" Please Enter the First Integer Value : ");
		Num1 = sc.nextInt();	
		
		System.out.print(" Please Enter the Second Integer Value : ");
		Num2 = sc.nextInt();
		
		while(Num2 != 0)
	    {
			Temp = Num2;
			Num2 = Num1 % Num2;
			Num1 = Temp;
	    }
		GCD = Num1;
		System.out.println("\n GCD  =  " + GCD);
	}
}

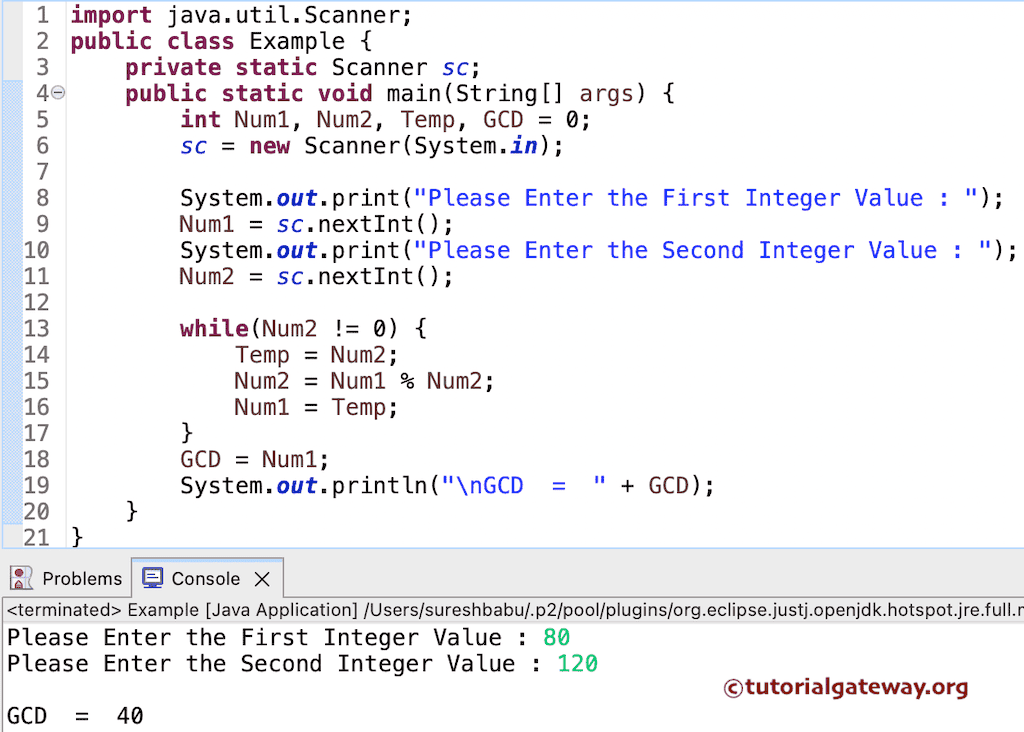
使用 While 循环 输出

不使用 Temp

此程序在不使用任何临时变量的情况下计算两个数的 gcd 或最大公约数。

import java.util.Scanner;

public class GOT3 {
	private static Scanner sc;
	public static void main(String[] args) 
	{
		int Num1, Num2, GCD = 0;
		sc = new Scanner(System.in);
		
		System.out.print(" Please Enter the First Integer Value : ");
		Num1 = sc.nextInt();	
		
		System.out.print(" Please Enter the Second Integer Value : ");
		Num2 = sc.nextInt();
		
		while(Num2 != 0)
	    {
			if(Num1 > Num2)
			{
				Num1 = Num1 - Num2;
			}
			else
			{
				Num2 = Num2 - Num1;
			}
	    }
		GCD = Num1;
		System.out.println("\n GCD  =  " + GCD);
	}
}

使用 Temp 值输出。

 Please Enter the First Integer Value : 27
 Please Enter the Second Integer Value : 360

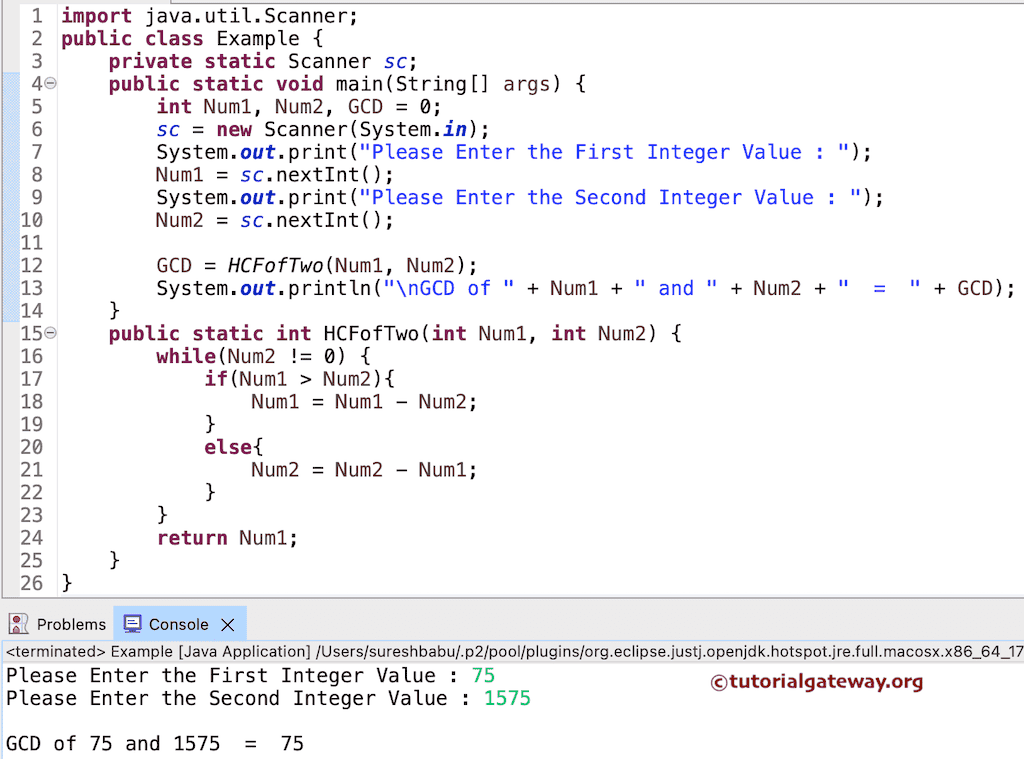
 GCD  =  9

使用函数查找两个数 GCD 的 Java 程序

此程序用于查找两个数的 gcd，与上面的示例相同。但是，这次我们将 Java 逻辑分开了，并将其放入一个单独的方法中。这有助于您非常有效地调试代码。

import java.util.Scanner;

public class GOT4 {
	private static Scanner sc;
	public static void main(String[] args) 
	{
		int Num1, Num2, GCD = 0;
		sc = new Scanner(System.in);
		
		System.out.print(" Please Enter the First Integer Value : ");
		Num1 = sc.nextInt();	
		
		System.out.print(" Please Enter the Second Integer Value : ");
		Num2 = sc.nextInt();
		
		GCD = HCFofTwo(Num1, Num2);
		
		System.out.println("\n GCD of " + Num1 + " and " + Num2 + "  =  " + GCD);
	}
	public static int HCFofTwo(int Num1, int Num2)
	{
		while(Num2 != 0)
	    {
			if(Num1 > Num2)
			{
				Num1 = Num1 - Num2;
			}
			else
			{
				Num2 = Num2 - Num1;
			}
	    }
		return Num1;
	}
}

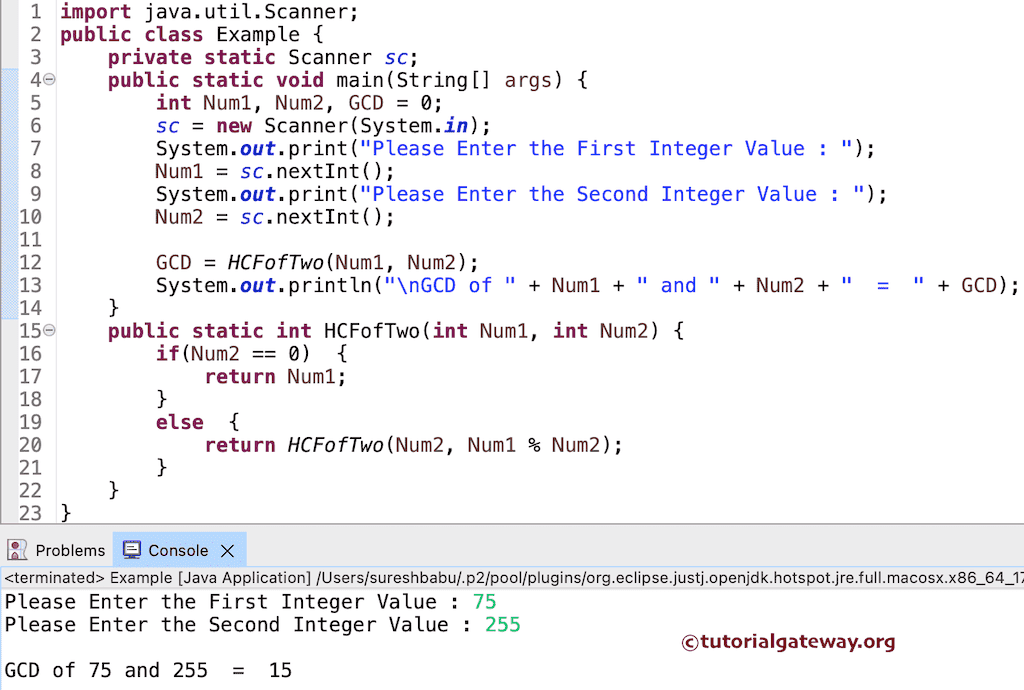
使用递归查找两个数 GCD 的 Java 程序

此程序通过递归调用 HCFofTwo 函数来计算最大公约数。我的意思是递归函数调用。

import java.util.Scanner;

public class GOT5 {
	private static Scanner sc;
	public static void main(String[] args) 
	{
		int Num1, Num2, GCD = 0;
		sc = new Scanner(System.in);
		
		System.out.print(" Please Enter the First Integer Value : ");
		Num1 = sc.nextInt();	
		
		System.out.print(" Please Enter the Second Integer Value : ");
		Num2 = sc.nextInt();
		
		GCD = HCFofTwo(Num1, Num2);
		
		System.out.println("\n GCD of " + Num1 + " and " + Num2 + "  =  " + GCD);
	}
	public static int HCFofTwo(int Num1, int Num2)
	{
		if(Num2 == 0)
		{
			return Num1;
		}
		else
		{
			return HCFofTwo(Num2, Num1 % Num2);
		}
	}
}

上述代码的输出是。