C++ 查找两个数的最小公倍数的程序

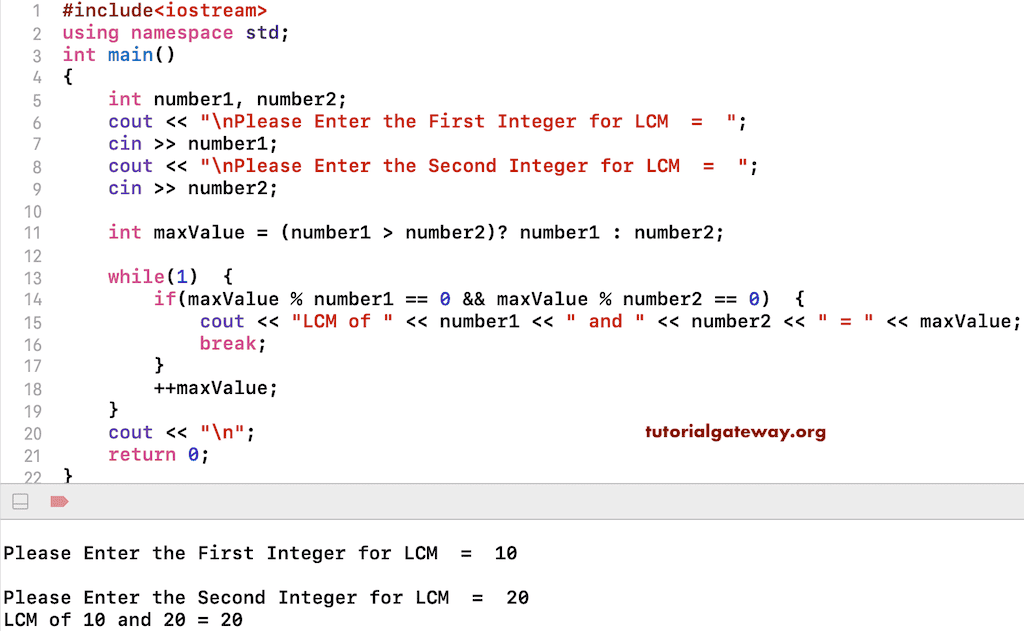
编写一个 C++ 程序，用一个例子来查找两个数的最小公倍数。LCM 是指两个或多个整数的最小公倍数。根据数学，它是能够完美整除该数（无余数）的最小整数（正数）。在这个例子中，我们使用 while 循环查找两个数的 LCM。

#include<iostream>
using namespace std;

int main()
{
	int number1, number2;
	
	cout << "\nPlease Enter the First Integer for LCM  =  ";
	cin >> number1;
	
	cout << "\nPlease Enter the Second Integer for LCM  =  ";
	cin >> number2;
	
	int maxValue = (number1 > number2)? number1 : number2;
	
	while(1)
	{
		if(maxValue % number1 == 0 && maxValue % number2 == 0)
		{
			cout << "LCM of " << number1 << " and " << number2 << " = " << maxValue;
			break;
		} 
		++maxValue;
	}
 	return 0;
}

C++ 使用 GCD 查找两个数 LCM 的程序

#include<iostream>
using namespace std;

int main()
{
	int number1, number2, lcm, gcd, temp;
	
	cout << "\nPlease Enter the First Integer =  ";
	cin >> number1;
	
	cout << "\nPlease Enter the Second Integer  =  ";
	cin >> number2;
	
	int a = number1;
	int b = number2;
	
	while(number2 != 0)
	{
		temp = number2;
		number2 = number1 % number2;
		number1 = temp;
	}
	gcd = number1;
	cout << "\nGCD of " << a << " and " << b << " = " << gcd;
	
	lcm = (a * b) / gcd;
	cout << "\nLCM of " << a << " and " << b << " = " << lcm;
 	return 0;
}

Please Enter the First Integer  =  15

Please Enter the Second Integer  =  40

GCD of 15 and 40 = 5
LCM of 15 and 40 = 120

在这个两个数 LCM 的程序中，long gcdOfTwoNumbers(long x, long y) 方法用于查找两个数的 GCD。接下来，我们使用该 GCD 来获得最小公倍数。请参考 C++ 程序。

#include<iostream>
using namespace std;

long gcdOfTwoNumbers(long x, long y)
{
	if(y == 0)
	{
		return x;
	}
	else
	{
		return gcdOfTwoNumbers(y, x % y);
	}
}

int main()
{
	int n1, n2, result;
	
	cout << "\nPlease Enter the First Value  =  ";
	cin >> n1;
	
	cout << "\nPlease Enter the Second Value  =  ";
	cin >> n2;
	
	long gcd = gcdOfTwoNumbers(n1, n2);

	cout << "\nGCD of " << n1 << " and " << n2 << " = " << gcd;
	
	lcm = (number1 * number2) / gcd;
	cout << "\nLCM of " << n1 << " and " << n2 << " = " << result;
 	return 0;
}

Please Enter the First Value  =  22

Please Enter the Second Value  =  120

GCD of 22 and 120 = 2
LCM of 22 and 120 = 1320