如何使用 for 循环、递归和函数编写 C 程序来计算级数 1³+2³+3³+….+n³ 的和,并附带示例。这个级数 1³+2³+3³+….+n³ 也被称为 C 语言中 n 个自然数的立方和。C 程序计算级数 1³+2³+3³+….+n³ 的和的数学公式 = ( n (n+1) / 6)²
C 程序计算级数 1³+2³+3³+….+n³ 的和
在此 C 程序中,用户被要求输入任何正整数。然后,使用该值,C 编译器将使用上述公式计算级数 1³+2³+3³+….+n³ 的和。
/* Sum of Cubes of n Natural Numbers */
#include <stdio.h>
#include <math.h>
int main()
{
int Number, Sum = 0;
printf("\n Please Enter any positive integer \n");
scanf(" %d",&Number);
Sum = pow(((Number * (Number + 1))/ 2), 2);
printf("\n The Sum of Series for %d = %d ",Number, Sum);
}
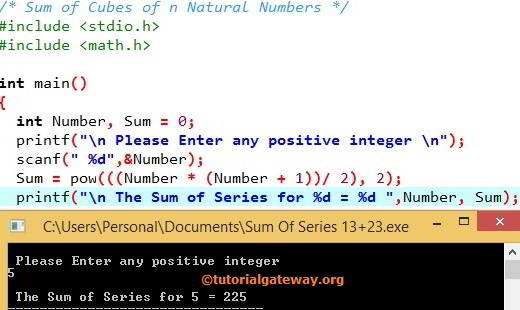
首先,我们声明了两个整型变量 Number 和 Sum。下一行,我们使用上述公式计算级数 1³+2³+3³+4³+5³ 的和。
Sum = pow (((Number * (Number + 1)) / 2), 2);
Sum = pow (((5 * (5 + 1)) / 2), 2);
Sum = pow (((5 * 6) / 2), 2);
Sum = pow ((30 / 2), 2);
Sum = pow (15, 2);
Sum = 15 * 15 = 225
C 语言的最终 printf 语句将把 Sum 作为输出打印出来。
printf("\n The Sum of Series for %d = %d ",Number, Sum);
因此,C 程序计算级数 1³+2³+3³+….+n³ 的和对于 5 的最终输出是 225。
C 程序使用 for 循环计算级数 1³+2³+3³+….+n³ 的和
如果您想在输出中显示级数 1³+2³+3³+4³ 的顺序,那么我们必须添加额外的 for 循环来显示,如下所示。
/* Sum of Cubes of n Natural Numbers */
#include <stdio.h>
#include <math.h>
int main()
{
int Number, i, Sum = 0;
printf("\nPlease Enter any positive integer \n");
scanf("%d",&Number);
Sum = pow(((Number * (Number + 1))/ 2), 2);
for(i =1; i<=Number;i++)
{
if (i != Number)
printf("%d^3 + ",i);
else
printf("%d^3 = %d ",i, Sum);
}
}
Please Enter any positive integer
4
1^3 + 2^3 + 3^3 + 4^3 = 100 main 函数中的 for 循环将遍历每个成员并显示输出。
for(i =1; i<=Number;i++)
{
if (i != Number)
printf(" %d^3 + ",i);
else
printf(" %d^3 = %d ",i, Sum);
}
在上面的输出中,用户输入的数字是 4,Sum = 100。现在编译器将进入 For 循环。
第一次迭代
i = 1,因此 for 循环中的条件 (i <= Number) 为 TRUE (1 <=4)。接下来,它会进入 if 条件 (i != Number)。这意味着 (1 != 4) – 这是 TRUE,因此它将输出 1³+。
i 增量到 2。它将执行相同的操作,直到 i 达到 4。当它等于 4 时,if 条件将失败,因此将打印 else 语句。
这个 C 程序的最终输出将是 1³+2³+3³+4³ = 100。
C 程序使用函数计算级数 1³+2³+3³+….+n³ 的和
此 C 程序使用 函数来计算级数 1³+2³+3³+….+n³ 的和。
/* Sum of Cubes of n Natural Numbers */
#include <stdio.h>
#include <math.h>
void Sum_Of_Series(int);
int main()
{
int Number;
printf("\n Please Enter any positive integer \n");
scanf("%d",&Number);
Sum_Of_Series(Number);
}
void Sum_Of_Series(int Number)
{
int i, Sum = 0;
Sum = pow (((Number * (Number + 1))/ 2), 2);;
for(i =1;i<=Number;i++)
{
if (i != Number)
printf("%d^3 + ",i);
else
printf(" %d^3 = %d ", i, Sum);
}
}
Please Enter any positive integer
6
1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 = 441程序的第一行是 用户定义函数的声明。
在 main() 函数中,
void Sum_Of_Series(int);
接下来,我们调用了用户定义的函数 Sum_Of_Series()。
Sum_Of_Series(Number);
当编译器到达 Sum_Of_Series() 时,它将跳转到函数定义进行计算。我们在上面的示例中已经解释了逻辑。
C 程序使用递归计算级数 1³+2³+3³+….+n³ 的和
此 C 程序允许输入 N 值,然后使用递归查找级数 1³+2³+3³+….+n³ 的和。
/* Sum of Cubes of n Natural Numbers */
#include <stdio.h>
int Sum_Of_Series(int);
int main()
{
int Number, Sum;
printf("\nPlease Enter any positive integer \n");
scanf("%d",&Number);
Sum =Sum_Of_Series(Number);
printf("\nSum of the Series = %d",Sum);
}
int Sum_Of_Series(int Number)
{
if(Number == 0)
return 0;
else
//Recursive Calling
return (Number * Number * Number) + Sum_Of_Series(Number-1);
}
Please Enter any positive integer
3
Sum of the Series = 36函数定义
在 Sum_Of_Series (Number) 函数中,如果用户输入的 Number 是 0,则函数将返回 0,否则它将返回。
(Number * Number * Number) + Sum_Of_Series(Number-1);
让我们将上述表达式分开以便更好地理解。
(Number * Number * Number) = 将数字乘以三次。
Sum_Of_Series(Number – 1) = 调用相同的函数,数字减 1。
从上面的输出中,用户输入的数字是 3,
级数 1³+2³+3³+….+n³ 递归 1 的和
Number = 3,大于 0 且 Sum 为 0,因此
Sum = (Number * Number) + Sum_Of_Series(Number-1)
Sum = (3 * 3 * 3) + Sum_Of_Series (3 – 1)
Sum = 27 + Sum_Of_Series (2)
Sum 值为 = 27
递归 2
Number = 2,大于 0 且 Sum 为 27。
Sum = (2 * 2 * 2) + Sum_Of_Series (2 – 1)
Sum = 8 + Sum_Of_Series (1)
Sum 值为:27 + 8 = 35
递归 3
Number = 1,大于 0 且 Sum 为 35,因此,
Sum = (1 * 1 * 1) + Sum_Of_Series (1 – 1)
Sum = 1 + Sum_Of_Series (0)
Sum 值为:35 + 1 = 36
递归 4
Number = 0,这意味着第一个 if 条件为 True,因此它将退出函数。Sum 的最终值为 36。我们必须使用一些条件来退出递归调用。如果您忘记了,那么 递归函数将执行无数次。