C 语言查找矩阵行列式的程序

如何编写 C 语言程序来查找矩阵的行列式，并附有示例。下图将向您展示此程序背后的数学公式。

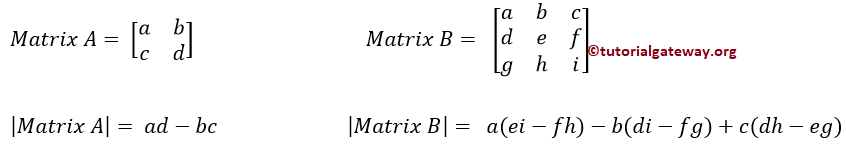
C 语言查找矩阵行列式的程序 – 2*2 示例

此程序允许用户输入 2*2 矩阵的行和列元素。接下来，我们将找到此矩阵的行列式。

/* Determinant of a 2 * 2 Matrix */
 
#include<stdio.h>
 
int main()
{
 	int rows, columns, a[2][2], Deter = 0;
  
 	printf("\n Please Enter the 2 * 2 Matrix Elements \n ");
 	for(rows = 0; rows < 2; rows++)
  	{
   		for(columns = 0;columns < 2; columns++)
    	{
      		scanf("%d", &a[rows][columns]);
    	}
  	}
     
	Deter = (a[0][0] * a[1][1]) - (a[0][1] * a[1][0]);
  	
  	printf("\n The Determinant of 2 * 2 Matrix = %d", Deter);
 	return 0;
}

 Please Enter the 2 * 2 Matrix Elements 
 10 20
30 40

 The Determinant of 2 * 2 Matrix = -200

在此程序中，我们使用 for 循环迭代 a[2][2] 矩阵中的每个单元格。for 循环内的条件 ((rows < i) 和 (columns < j)) 将确保编译器不会超出 矩阵的限制。否则，矩阵将溢出。

for 循环中的 C 语言 scanf 语句将用户输入的值存储在每个单独的数组元素中，例如 a[0][0]、a[0][1]、……。

for(rows = 0; rows < i; rows++).
{
  for(columns = 0; columns < j; columns++)
   {
     scanf("%d", &a[rows][columns]);
   }
}

下一行，我们正在计算行列式

Determinant = (a[0][0] * a[1][1]) - (a[0][1] * a[1][0]);

用户输入的数组 a[2][2] = {{10, 20}, {30, 40}}

行列式 = (a[0][0] * a[1][1]) – (a[0][1] * a[1][0])

= (10 * 40) – (20 * 30)

行列式 = (400) – (600) = -200

C 语言查找矩阵行列式的程序 – 3*3 示例

此程序与上面的示例类似，但这次我们正在查找 3*3 矩阵的行列式。

/* Determinant of a 3 * 3 Matrix */
 
#include<stdio.h>
 
int main()
{
 	int rows, columns, a[3][3];
	int x, y, z, Determinant = 0;
  
 	printf("\n Please Enter the 3 * 3 Matrix Elements \n");
 	for(rows = 0; rows < 3; rows++)
  	{
   		for(columns = 0;columns < 3; columns++)
    	{
      		scanf("%d", &a[rows][columns]);
    	}
  	}
  	
    x = (a[1][1] * a[2][2]) - (a[2][1] * a[1][2]);
    y = (a[1][0] * a[2][2]) - (a[2][0] * a[1][2]);
    z = (a[1][0] * a[2][1]) - (a[2][0] * a[1][1]);
	
	Determinant = (a[0][0] * x) - (a[0][1] * y) + (a[0][2] * z);
  	
  	printf("\n The Determinant of 3 * 3 Matrix = %d", Determinant);
 	return 0;
}

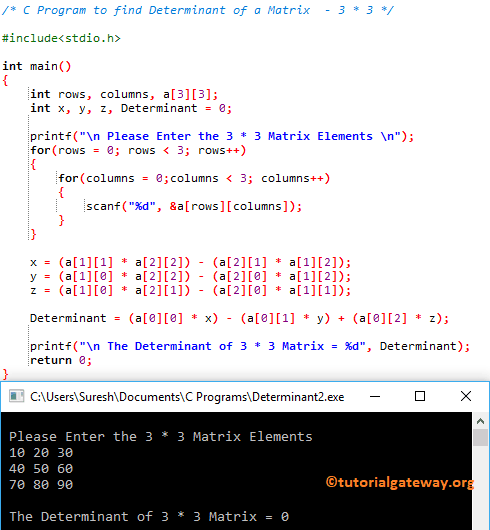
在此程序示例中，用户输入的数组 a[3][3] = {{10, 20, 30}, {40, 50, 60}, {70, 80, 90}}

x = (a[1][1] * a[2][2]) – (a[2][1] * a[1][2])

x = (50 * 90) – (80 * 60)

x = 4500 – 4800

x = -300

y = (a[1][0] * a[2][2]) – (a[2][0] * a[1][2])

y = (40 * 90) – (70 * 60)

y = 3600 – 4200

y = -600

z = (a[1][0] * a[2][1]) – (a[2][0] * a[1][1])

z = (40 * 80) – (70 * 50)

z = (3200) – (3500)

z = -300

行列式 = (a[0][0] * x) – (a[0][1] * y) + (a[0][2] * z)

= (10 * -300) – (20 * -600) + (30 * -300)

= (-3000) – (-12000) + (-9000)

行列式 = -3000 + 12000 – 9000 = 0