C程序检查矩阵是否为对称矩阵

如何编写C程序来检查矩阵是否为对称矩阵，并附带示例。任何方阵称为对称矩阵，如果一个矩阵等于其转置矩阵。

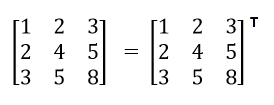
C程序检查矩阵是否为对称矩阵示例

此程序允许用户输入矩阵的行数和列数。接下来，我们将使用For循环检查给定的矩阵是否为对称矩阵。

/* Check Matrix is a Symmetric Matrix or Not */
 
#include<stdio.h>
 
int main()
{
 	int i, j, rows, columns, a[10][10], b[10][10], Count = 1;
  
 	printf("\n Please Enter Number of rows and columns  :  ");
 	scanf("%d %d", &i, &j);
 
 	printf("\n Please Enter the Matrix Elements \n");
 	for(rows = 0; rows < i; rows++)
  	{
   		for(columns = 0;columns < j;columns++)
    	{
      		scanf("%d", &a[rows][columns]);
    	}
  	}
   	//Transpose of matrix 
 	for(rows = 0; rows < i; rows++)
  	{
   		for(columns = 0;columns < j; columns++)
    	{
      		b[columns][rows] = a[rows][columns];
    	}
  	}
     
 	for(rows = 0; rows < i; rows++)
  	{
   		for(columns = 0; columns < j; columns++)
    	{
    		if(a[rows][columns] != b[rows][columns])
    		{
    			Count++;  
				break;  		
			}
   	 	}
  	}
  	if(Count == 1)
  	{
  		printf("\n The Matrix that you entered is a Symmetric Matrix ");
	}
	else
	{
		printf("\n The Matrix that you entered is Not a Symmetric Matrix ");
	}
  	
 	return 0;
}

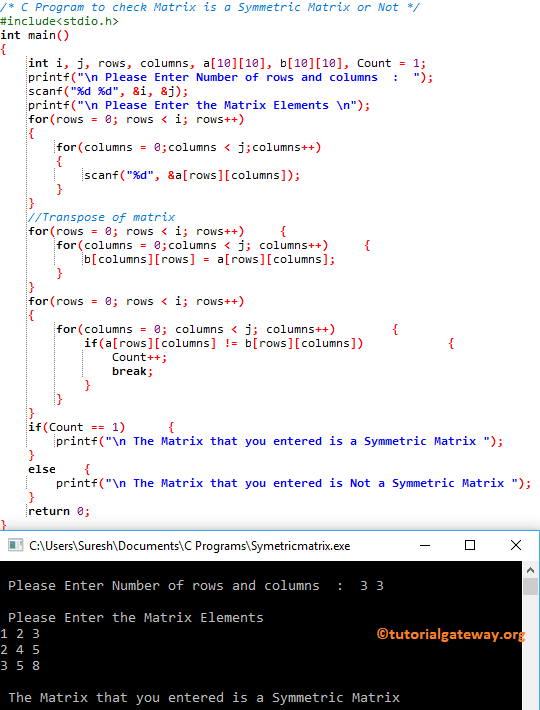
在此“检查矩阵是否为对称矩阵”程序中，我们声明了大小为10*10的二维数组乘法。

此程序中的以下语句要求用户输入矩阵的大小（行数和列数。例如，2行，2列= a[2][2]）。

printf("\n Please Enter Number of rows and columns  :  ");
scanf("%d %d", &i, &j);

接下来，我们使用for循环遍历a[2][2]矩阵中的每个元素。for循环中的条件（（rows < i）和（columns < j））确保编译器不超出矩阵限制。否则，矩阵将溢出。C编程C Programming for循环中的scanf语句会将用户输入的值存储在每个单独的数组元素中，例如a[0][0]，a[0][1]，……。

for(rows = 0; rows < i; rows++).
{
  for(columns = 0; columns < j; columns++)
   {
     scanf("%d", &a[rows][columns]);
   }
}

在下一行，我们使用For循环来转置此矩阵。我建议您参考转置矩阵文章来理解它。

for(rows = 0; rows < i; rows++)  	
{
   	for(columns = 0;columns < j; columns++)    	
        {
      		b[columns][rows] = a[rows][columns];
    	}
}

接下来，我们尝试检查矩阵中的每个元素是否等于转置矩阵。

for(rows = 0; rows < i; rows++)
{
   	for(columns = 0; columns < j; columns++)
    	{
    		if(a[rows][columns] != 1 && a[columns][rows] != 0)
    		{
    			Flag = 0;
    			break;
		}
   	}
}

让我用其他值试试这个程序。

 Please Enter Number of rows and columns  :  3 3

 Please Enter the Matrix Elements 
10 20 30
40 50 60
70 80 90

 The Matrix that you entered is Not a Symmetric Matrix